Overview of “Thomas Calculus: Early Transcendentals”
Thomas Calculus: Early Transcendentals is a comprehensive guide for calculus education‚ covering functions‚ limits‚ derivatives‚ and integrals. Tailored for modern learners‚ it’s available as a PDF download.
Thomas Calculus: Early Transcendentals is a renowned textbook designed to introduce students to the fundamental concepts of calculus. It emphasizes the early introduction of transcendental functions‚ providing a solid foundation for understanding derivatives‚ integrals‚ and their applications. The book is structured to enhance conceptual understanding‚ with clear explanations‚ detailed examples‚ and practice exercises. Authored by Maurice D. Weir‚ Joel Hass‚ and George B. Thomas‚ it is available in multiple editions‚ including the 12th‚ 14th‚ and 15th‚ and can be accessed as a PDF for convenient learning.
1.2 Authors and Editions
Thomas Calculus: Early Transcendentals is authored by Maurice D. Weir‚ Joel Hass‚ and George B. Thomas‚ building on the original work by George B. Thomas Jr. The book is available in multiple editions‚ including the 12th‚ 14th‚ and 15th editions‚ each offering enhanced content and improved clarity. The 12th edition‚ for instance‚ includes an ISBN of 978-0-321-58876-0. These editions cater to modern learners‚ with resources like PDF downloads and online platforms for easy access‚ ensuring flexibility and convenience for students and educators alike.
1.3 Key Features of the Textbook
Thomas Calculus: Early Transcendentals is a comprehensive textbook designed to enhance conceptual understanding. It introduces transcendental functions early‚ aligning with modern teaching methods. The book includes detailed chapters on functions‚ limits‚ derivatives‚ and integrals‚ with a strong emphasis on real-world applications. Available in multiple editions‚ it offers PDF downloads for convenience. Resources like MyLab Math integration and Just-in-Time algebra and trigonometry reviews support student learning. The electronic version is accessible‚ though some content may be restricted due to rights limitations‚ ensuring flexibility for both students and instructors.

Table of Contents
The table of contents includes chapters on functions‚ combining functions‚ trigonometric functions‚ limits‚ derivatives‚ and integrals‚ each with detailed subsections in the PDF version.
2.1 Chapter 1: Functions
Chapter 1 introduces the fundamental concept of functions‚ exploring their definitions‚ properties‚ and graphical representations. It covers functions and their graphs‚ combining functions through operations‚ and transformations such as shifting and scaling. The chapter also provides a solid foundation for understanding the behavior of functions‚ essential for advanced calculus topics. The PDF version of the textbook includes detailed explanations‚ examples‚ and exercises to help students master these concepts. This section is crucial for building a strong base in calculus and its applications.
2.2 Chapter 2: Combining Functions
Chapter 2 focuses on combining functions through various operations‚ including addition‚ subtraction‚ multiplication‚ and division. It also explores shifting and scaling of graphs‚ which are essential techniques for understanding function transformations. The chapter provides detailed examples and exercises to help students master these concepts; The PDF version of the textbook includes visual aids and practice problems to reinforce learning. This section builds on the foundation established in Chapter 1‚ preparing students for more complex topics in calculus. The exercises emphasize practical applications of combined functions.
2.3 Chapter 3: Trigonometric Functions
Chapter 3 delves into trigonometric functions‚ covering their definitions‚ properties‚ and applications. It explores sine‚ cosine‚ and tangent functions‚ along with their graphs and inverses. The chapter emphasizes understanding periodicity and trigonometric identities‚ which are crucial for calculus. The PDF version includes detailed graphs and practice exercises to aid comprehension. This section is vital for students to grasp concepts like arc length and angular motion‚ setting the stage for advanced calculus topics. The clear explanations and visual aids make complex ideas accessible.
2.4 Chapter 4: Limits
Chapter 4 focuses on limits‚ a foundational concept in calculus. It introduces the idea of evaluating functions as they approach specific values‚ emphasizing the formal definition of a limit. The chapter covers one-sided limits‚ infinite limits‚ and limits at infinity‚ with practical examples. The PDF version includes detailed explanations and practice problems to help students master this crucial topic. Understanding limits is essential for progressing in calculus‚ as it forms the basis for derivatives and continuity. The text provides clear‚ step-by-step guidance to ensure comprehension.
2.5 Chapter 5: Derivatives
Chapter 5 introduces the concept of derivatives‚ a cornerstone of calculus. It explores the definition of a derivative‚ rules for differentiation‚ and applications in optimization and related rates. The chapter emphasizes the relationship between derivatives and the slope of tangent lines‚ with detailed examples and exercises. The PDF version provides clear explanations and visual aids to help students grasp this fundamental concept. Understanding derivatives is crucial for analyzing functions and their behavior‚ making this chapter a key part of the learning process in calculus.
2.6 Chapter 6: Integrals
Chapter 6 delves into integrals‚ focusing on their definition‚ properties‚ and applications. It covers indefinite integrals‚ definite integrals‚ and the Fundamental Theorem of Calculus‚ which links integration and differentiation. The chapter also explores techniques like substitution and integration by parts. Practical applications‚ such as calculating area under curves and solving accumulation problems‚ are emphasized. The PDF format ensures clear presentation of integral rules and examples‚ making complex concepts accessible for students to master integral calculus effectively. This chapter is vital for understanding rates of change and accumulation.

Learning Resources
The textbook offers comprehensive learning resources‚ including PDF downloads and online platforms‚ to support student understanding and problem-solving in calculus‚ ensuring accessibility and enriched learning experiences.
3.1 Student Solutions Manual
The Student Solutions Manual provides detailed‚ worked-out solutions to selected exercises‚ helping students grasp problem-solving techniques and understand key concepts. It covers topics like limits‚ derivatives‚ and integrals‚ offering step-by-step explanations for complex problems. This resource is invaluable for self-study‚ allowing learners to check their work and improve their understanding of calculus. The manual is particularly useful for reinforcing lessons and identifying areas that require additional practice. It serves as a companion tool to enhance learning and mastery of the subject matter effectively.
3.2 Just-in-Time Algebra and Trigonometry Reviews
The textbook includes Just-in-Time reviews of algebra and trigonometry‚ ensuring students have a strong foundation before tackling calculus concepts. These reviews are strategically placed throughout the chapters‚ providing concise refreshers on essential topics like functions‚ equations‚ and identities. This feature helps bridge gaps in prerequisite knowledge‚ enabling students to focus on calculus without getting stuck on rusty skills. The reviews are self-contained‚ making it easy for learners to quickly revisit key concepts and apply them to current problems seamlessly.
3.3 MyLab Math Integration
The textbook is seamlessly integrated with MyLab Math‚ Pearson’s online learning platform. This integration provides students with a wealth of digital resources‚ including interactive tutorials‚ quizzes‚ and homework assignments. MyLab Math offers personalized learning paths‚ real-time feedback‚ and a comprehensive gradebook. It aligns perfectly with the textbook content‚ ensuring a cohesive learning experience. Students can access additional practice problems‚ video lectures‚ and simulations to deepen their understanding. This integration enhances engagement and helps students master calculus concepts efficiently‚ both in and out of the classroom.
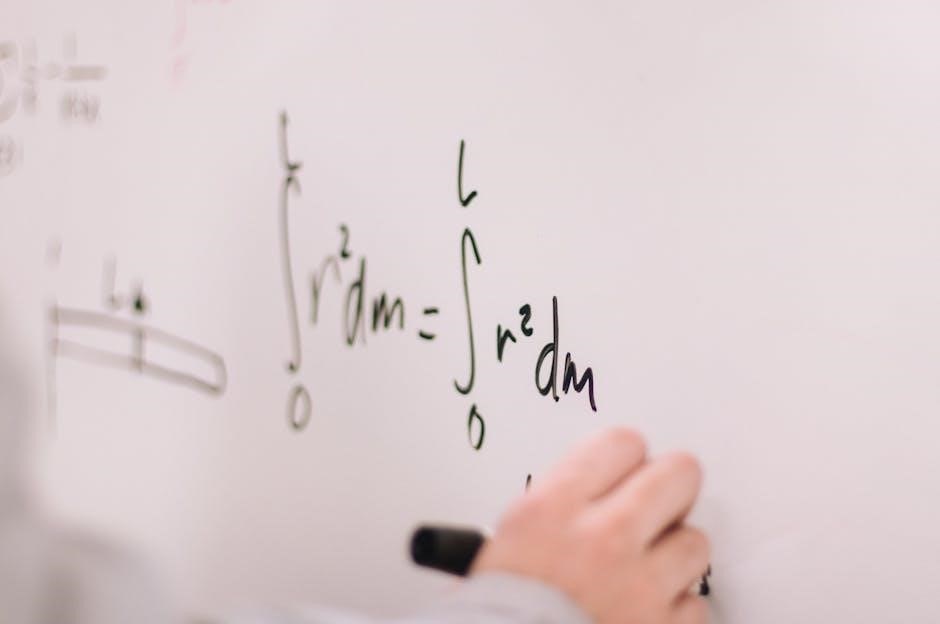
Key Topics Covered
This section outlines the core mathematical concepts explored in the textbook‚ including calculus fundamentals‚ functions‚ limits‚ derivatives‚ integrals‚ series‚ vectors‚ and their practical applications.
4.1 Real Number System
The textbook begins with a thorough exploration of the real number system‚ emphasizing its structure and properties. It covers inequalities‚ intervals‚ and properties of real numbers‚ such as commutativity and associativity. The authors also delve into the density of real numbers and their representation on the number line. This foundational chapter ensures students grasp the essential concepts necessary for advanced calculus topics‚ providing a robust mathematical framework for understanding limits‚ derivatives‚ and integrals later in the text. Key properties like closure and the least upper bound are highlighted.
4.2 Cartesian Coordinates
The textbook introduces Cartesian coordinates as a fundamental framework for analyzing functions and their graphical representations. It explains the x and y axes‚ plotting points‚ and interpreting graphs of equations. This section highlights the importance of understanding coordinate geometry in calculus‚ particularly for visualizing functions‚ limits‚ and derivatives. Students learn to interpret slopes‚ intercepts‚ and symmetry‚ building a visual foundation for advanced topics like parametric equations and polar coordinates later in the text. Clear diagrams and examples are provided to enhance comprehension of this critical concept.
4.3 Basic Concepts of Calculus
The textbook lays a solid foundation in the core principles of calculus‚ starting with limits‚ the cornerstone of the subject. It progresses to derivatives‚ explaining rates of change and slopes of tangent lines‚ and integrals‚ covering accumulation and area under curves. The text emphasizes the relationship between derivatives and integrals through the Fundamental Theorem of Calculus. Clear explanations and examples guide students through these essential ideas‚ ensuring a strong grasp of the basics before advancing to more complex topics. This section is pivotal for building a lasting understanding of calculus.

Importance of Early Transcendentals
Introducing transcendental functions early in calculus enhances students’ ability to solve modern‚ real-world problems‚ preparing them for practical applications in engineering‚ physics‚ and advanced sciences.
5.1 Approach to Transcendental Functions
The early introduction of transcendental functions in Thomas Calculus streamlines the learning process by integrating exponential‚ logarithmic‚ and trigonometric functions with core calculus concepts; This approach ensures students grasp how these functions behave under differentiation and integration‚ preparing them for advanced applications in physics‚ engineering‚ and other STEM fields. By addressing transcendental functions early‚ the textbook avoids fragmented learning‚ allowing for a cohesive understanding of their properties and roles in modeling real-world phenomena.
5.2 Benefits for Modern Learners
The early transcendentals approach in Thomas Calculus equips modern learners with a strong foundation in calculus‚ essential for STEM disciplines. By introducing transcendental functions early‚ students can apply these concepts seamlessly in subsequent chapters‚ enhancing problem-solving skills. This method aligns with the demands of modern education‚ preparing learners for real-world applications in fields like engineering‚ physics‚ and data science.
The textbook’s integration with digital resources‚ such as MyLab Math‚ further supports interactive and personalized learning‚ catering to diverse learning styles and preferences.

Availability and Access
The Thomas Calculus: Early Transcendentals PDF is widely available through official publishers‚ online retailers‚ and educational platforms‚ ensuring easy access for students and educators worldwide.
6.1 PDF Downloads
The Thomas Calculus: Early Transcendentals PDF is readily available for download from various sources‚ including official publishers and educational platforms. Students can access the full textbook in digital format‚ offering convenience and portability. The PDF version allows for easy searching‚ highlighting‚ and annotation‚ making it a popular choice for modern learners. However‚ it is essential to ensure that downloads are obtained from legitimate sources to avoid copyright infringement. Official publisher websites and authorized retailers provide secure and legal access to the PDF‚ ensuring quality and completeness of the content.
6.2 Online Platforms and Resources
The Thomas Calculus: Early Transcendentals is accessible through various online platforms‚ such as Pearson’s official website and MyLab Math. These platforms offer digital access to the textbook‚ along with supplementary resources like interactive tutorials‚ video lectures‚ and practice exercises. Additionally‚ online forums and study groups provide opportunities for collaboration and problem-solving. Many universities and libraries also offer e-book versions‚ making it easier for students to access the material remotely. These resources enhance learning by providing a comprehensive and flexible study experience.

Study Tips
Focus on understanding core concepts‚ practice regularly‚ and review problem-solving strategies. Utilize visual aids and seek help when needed to grasp complex topics effectively.
7.1 Mastering Key Concepts
Mastering key concepts in Thomas Calculus: Early Transcendentals requires a deep understanding of foundational topics like functions‚ limits‚ derivatives‚ and integrals. Focus on definitions‚ theorems‚ and their applications. Regular practice helps solidify these concepts‚ while breaking down complex problems into simpler parts enhances comprehension. Use visual aids like graphs and videos to supplement learning. Applying concepts to real-world problems strengthens retention. Consulting the Student Solutions Manual and online resources provides additional support for challenging topics‚ ensuring a robust grasp of calculus fundamentals.
7.2 Effective Use of Practice Exercises
Effective use of practice exercises in Thomas Calculus: Early Transcendentals involves working through problems systematically. Start with basic exercises to build familiarity with concepts‚ then progress to more challenging ones. Pay attention to areas where mistakes occur‚ as these indicate weak points. Use the Student Solutions Manual to verify answers and understand problem-solving strategies. Regular practice reinforces understanding and improves problem-solving skills‚ ensuring mastery of calculus concepts. Consistency is key to long-term success in the course.
7.3 Utilizing Visual Aids
Visual aids in Thomas Calculus: Early Transcendentals are essential for understanding complex concepts. The textbook includes detailed graphs‚ charts‚ and diagrams to illustrate key ideas like function behavior and calculus principles. These tools help students visualize abstract relationships‚ making them easier to grasp. Interactive elements in the PDF‚ such as 3D graphs and simulations‚ enhance engagement. By using these resources‚ students can better understand and retain the material‚ supporting various learning styles and fostering a more effective learning experience.

Common Challenges
Students often struggle with understanding limits‚ mastering integration techniques‚ and applying calculus concepts to real-world problems. These challenges require strong foundational knowledge and practice to overcome effectively.
8.1 Understanding Limits and Continuity
Understanding limits and continuity is fundamental yet challenging. Students often struggle with conceptualizing one-sided limits‚ infinite limits‚ and the formal epsilon-delta definition. Continuity‚ while intuitive‚ becomes complex with removable and jump discontinuities. Visualizing function behavior near points of discontinuity and applying limit properties requires careful practice. These concepts are crucial for derivatives and integrals‚ making them essential to master despite the initial difficulty.
8.2 Mastering Integration Techniques
Mastering integration techniques is a critical yet challenging aspect of calculus. Students often find it difficult to choose the appropriate method for a given problem‚ whether substitution‚ integration by parts‚ or partial fractions. Trigonometric integrals and improper integrals add further complexity. The textbook provides detailed explanations and practice exercises to help students build proficiency. Regular practice and reviewing examples are essential to overcome these challenges and apply integration effectively in various mathematical and real-world scenarios.
8.3 Applications of Calculus in Real-World Scenarios
Calculus has vast applications in real-world scenarios‚ making it a cornerstone of modern science and engineering. It is used to model motion in physics‚ optimize systems in economics‚ and understand growth in biology. For instance‚ calculus helps predict population dynamics‚ analyze fluid flow‚ and design electronic circuits. These practical examples highlight the importance of mastering calculus concepts. The textbook emphasizes these applications to illustrate how mathematical theories solve real-world problems‚ bridging academia with practical relevance.

Comparison with Other Editions
The 15th edition of Thomas’ Calculus: Early Transcendentals includes updated problem sets‚ enhanced digital integration‚ and improved clarity compared to earlier editions‚ offering a refined learning experience.
9.1 Differences Between 14th and 15th Editions
The 15th edition of Thomas’ Calculus: Early Transcendentals introduces refined problem sets‚ improved explanations‚ and enhanced visual aids compared to the 14th edition. It incorporates updated technology integration‚ particularly with MyLab Math‚ offering a more interactive learning experience. Additionally‚ the 15th edition streamlines complex topics like limits and continuity‚ making them more accessible for students. These updates ensure the textbook remains a cutting-edge resource for calculus education‚ addressing modern teaching and learning needs effectively.
9.2 Updates in the 12th Edition
The 12th edition of Thomas’ Calculus: Early Transcendentals introduced enhanced clarity in explanations‚ particularly in differentiation and integration techniques. It featured expanded problem sets with more real-world applications‚ improving practical understanding. Additionally‚ the 12th edition incorporated improved visual aids‚ such as graphs and illustrations‚ to better assist students in grasping complex concepts. The edition also emphasized just-in-time algebra and trigonometry reviews‚ ensuring students could refresh foundational skills as needed. These updates strengthened the textbook’s effectiveness in supporting student success in calculus.

Educational Impact
Thomas’ Calculus: Early Transcendentals has significantly shaped STEM education by providing a comprehensive‚ clear framework for understanding calculus. Its detailed explanations and exercises have helped students build a strong foundation in mathematical analysis‚ enabling them to tackle complex problems in science‚ engineering‚ and economics. The textbook’s structured approach has made it a trusted resource for both students and instructors‚ fostering academic success and practical application. Its impact on calculus education remains unparalleled.
10.1 Role in STEM Education
Thomas’ Calculus: Early Transcendentals plays a pivotal role in STEM education by providing a rigorous foundation in calculus‚ essential for physics‚ engineering‚ and computer science. Its clear explanations and practical examples help students grasp complex concepts‚ enabling them to apply mathematical principles to real-world problems. The textbook’s emphasis on problem-solving and critical thinking prepares learners for advanced studies and careers in STEM fields‚ making it an indispensable resource for academic and professional development.
10.2 Feedback from Students and Instructors
Students and instructors widely praise Thomas’ Calculus: Early Transcendentals for its clarity and comprehensive coverage. Many students appreciate the textbook’s intuitive explanations and abundance of practice problems‚ which aid in mastering complex concepts. Instructors commend its logical structure and integration of modern tools‚ enhancing both teaching and learning experiences. However‚ some users note the material’s density and suggest additional visual aids could improve comprehension. Overall‚ the feedback highlights the book’s effectiveness in fostering a deep understanding of calculus.
